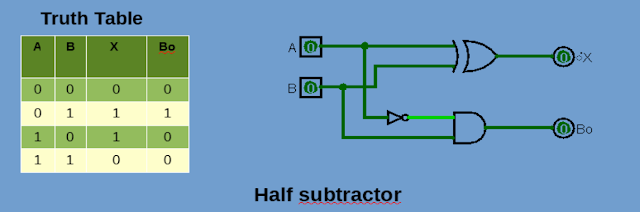
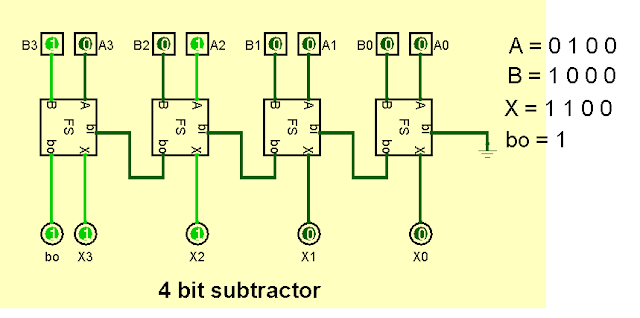
การสร้าง Symbol library ใหม่ สำหรับ Eeschema
วิธีที่ 1 สร้างด้วย schematic library editor
วิธีนี้เหมาะสำหรับการเอา symbol library ที่มีอยู่แล้วมาแก้ไข แล้ว Save ในชื่อ library ใหม่ เช่น สมมุติเราจะสร้าง IC ตัวใหม่ที่มีจำนวน ขาเท่ากับ IC555 ก็ให้เปิด symbol library ของ IC555 มาแก้ไขเปลี่ยนแปลงชื่อ Pin เอา การแก้ไขดังกล่าวไม่เกี่ยวกับ footprint แต่อย่างไร เนื่องจากมันอาศัย CvPCB ในการเชื่อมโยง footprint เข้ากับ symbol
วิธีนี้ทำโดยการคลิ๊กที่ schematic library editor Icon ใน Kicad Manager หรือ Tools--> library editor ใน Eeschema จะไม่ขอกล่าวในที่นี้ เนื่องจากทำได้ง่าย แต่เสียเวลา เหมาะกับการแก้ไขอุปกรณ์ที่มีจำนวน Pin น้อยๆ และสามารถหาดูวิธีการทำได้ในคู่มือ หรือบนอินเตอร์เน็ต
 |
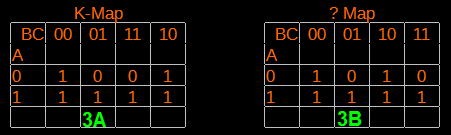
| รูปที่ 1 วิธีเรียกใช้ Library editor |
ข้อดี : -
• แก้ไขได้รวดเร็ว และสามารถเห็นหน้าตา หรือ Symbol ขณะที่แก้ไขได้
• ปรับขนาด กว้าง , ยาว ของ symbol และระยะห่างของ Pin ได้ตามใจ
• สร้าง symbol ที่มีรูปร่างต่างๆ ได้หลากหลาย เช่น ทรานซิสเตอร์, เสาอากาศ, op-amp เป็นต้น
ข้อเสีย :-
• การแก้ไขอุปกรณ์ ที่มีหลายขา เช่น IC ใน Package DIL,QFP,PGA, LCC เป็นต้น เสียเวลามาก และต้องเลือกเอาต้นแบบที่คล้ายกันมากๆ มาแก้ไข ซึ่งต้องเสียเวลาหาต้นแบบใน library นาน
• ถ้าจะสร้างใหม่ตั้งแต่ต้น ก็เสียวลานานในการวางตำแหน่ง PIN วาด Symbol
• บางครั้งจะมีปัญหา Hidden pin จาก symbol ที่เราเอามาแก้ไข
• ทุกครั้งที่จะแก้ไข จะมีหน้าต่าง popup ขึ้นมาให้ใส่ค่า ทุกครั้งไป ทำให้ช้าขึ้นไปอีก
วิธีที่ 2 สร้างด้วย Kicad Quicklibary เว็บไซท์
 |
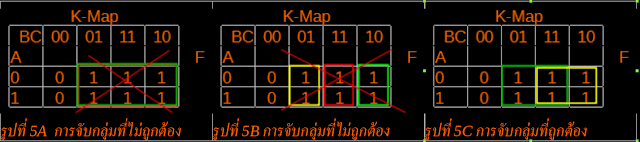
| รูปที่ 2 หน้าตาของ KiCad quicklib |
โดยให้เข้าไปที่ http://kicad.rohrbacher.net/quicklib.php จะมีหน้าตาดังรูปที่ 2 เมื่อคลิ๊กที่ Assign Pin จะโหลดหน้าต่างใหม่ ให้ตั้งชื่อ Pin, Type, Name และ Format
ข้อดี : -
• แก้ไขได้รวดเร็ว
• ปรับขนาด กว้าง , ยาว ของ symbol และระยะห่างของ Pin ได้ตามใจ
• ไม่จำเป็นต้องติดตั้งโปรแกรมเพิ่มเติม
• เห็นรายละเอียดต่างๆ ของ Pin ที่สร้าง
ข้อเสีย :-
• สร้างได้แต่อุปกรณ์ที่มี Package ตามที่แสดงในเวบ คือมี Package สี่เหลี่ยมเท่านั้น
• ถ้า IC มีจำนวนขาเยอะๆ เช่น 40 ขาขึ้นไป ก็ยังใช้เวลานานในการใส่ข้อมูล
• ต้องออนไลน์
วิธีที่ 3 สร้างด้วย Kipart
Kipart เป็น Python script ที่ใช้ในการสร้าง Kicad symbol library จาก CSV file มันมีความสามารถที่จะอ่าน CSV files หลาย ไฟล์ แล้วแปลงเป็น Kicad symbol library ได้ในครั้งเดียว
วิธีนี้ใช้สร้าง symbol library ที่มี package ที่แน่นอนเช่น เดียวกับการสร้างด้วย Kicad quicklib ในวิธีที่ 2 แต่รวดเร็วกว่ามาก โดยเฉพาะ IC ที่มีขาเยอะๆ แต่ต้องมี datasheet หรือ pin description หรือ pin functions ของ IC นั้นๆ
ข้อดี : -
• สร้างอุปกรณ์ที่มีจำนวน Pin เยอะๆ ได้รวดเร็วมาก
• สามารถสร้าง symbol library ได้หลายๆ ตัวในเวลาเดียวกัน เช่น ใน 74xx library ถ้าเปิดเข้าไปดู จะเห็นได้ว่ามี IC ตระกูล 74xx ไม่น้อยกว่า 100 ตัว
• ตรวจสอบความถูกต้องได้ และแก้ไขใหม่ได้ง่าย (สร้างโดยวิธีที่ 1 มักจะมีปัญหา Hidden Pin)
• ไม่ต้องออนไลน์เมื่อใช้ Kipart
ข้อเสีย :-
• ต้องติดตั้งโปรแกรมเพิ่มเติม
• ปรับขนาด กว้าง , ยาว ของ symbol และระยะห่างของ Pin ยาก ถึงไม่ได้เลย
• ต้องเรียนรู้คำสั่งของ Kipart ถ้าจะให้มันทำงานแบบเต็มความสามารถที่มี
• สร้างได้แต่ symbol ที่มีลักษณะสี่เหลี่ยม
โดยสิ่งที่จำเป็นต้องมี มีดังนี้
1. datasheet หรือ pinout ของอุปกรณ์ที่จะสร้าง symbol library
2. โปรแกรมที่สร้าง CSV file ได้ เช่น Spread sheet ทั้งหลาย
3. Python compiler
การติดตั้ง Kipart
1. ถ้าเครื่องเราไม่มี Python อยู่ ก่อน เช่น Windows OS ต้องไปโหลด Python มาติดตั้งจากที่นี่ https://www.python.org/downloads/ เลือกเอาว่าจะใช้แบบไหน Pyton 3X, Python 2X, ทำงานบนWindos 64bit หรือ Windows 32 bit ก็ได้แล้วแต่สะดวก ไม่มีผลต่อการใช้งาน เพราะมันจะ compile Kipart ให้เป็น Executable file (*.exe)
ตรวจสอบให้แน่ใจว่า Python ของเราถูก Add path ไว้แล้วโดยใช้คำสั่งต่อไปนี้ ใน Command shell
c:\python -v กรณีติดตั้ง python 2x
c:\python –version กรณีติดตั้ง python 3x
ข้อควรระวัง
• ในการติดตั้ง Python ต้องเลือก ติดตั้งสำหรับ All users และ Add Python path
• กรณีติดตั้ง Python 2X ต้องเลือก Customize installation
 |
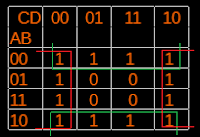
| รูปที่ 3 ตัวเลือกการติดตั้งของ Python 2x |
2.ถ้าเครื่องเรามี Python อยู่ก่อนแล้ว เช่น Linux OS ทั้งหลาย และเชื่อมต่ออินเตอร์เน็ตอยู่ ก็ติดตั้งได้เลยโดย ใช้คำสั่งต่อไปนี้ (ไม่จำเป็นต้องไป download source มา compile เอง)
> pip install kipart หรือ
> easy_install kipart
มันจะไปหา Kipart เวอร์ชั่นล่าสุดจากอินเตอร์เน็ต มาให้โดยและติดตั้งโดยอัตโนมัติ
หมายเหตุ :
ทั้ง โปรแกรม pip และ easy_install มีอยู่แล้วใน c:\kicad\bin แต่ไม่แน่ใจว่ามันจะสามารถไปดึง Kipart จาก Github มาติดตั้งได้เลยหรือไม่ เนื่องจากเครื่องที่ใช้มี Python อยู่ก่อนแล้ว เมื่อเรียกใช้ Pip หรือ Easy_install มันจะถูกเรียกจาก Pip หรือ Easy_install ใน python directory
ขั้นตอนการสร้าง symbol library ด้วย Kipart ให้ทำตาม Video นี้
หมายเหตุ
ถ้าต้องการแสดงสัญญลักษณ์ Active Low เช่น ENABLE บน symbol (มีขีดข้างล่าง บอก Active Low)ให้ใส่คำหรือเครื่องหมาย inverted, inv, ~, หรือ # นำหน้า
ขั้นตอนในการใช้ Kipart command มีดังนี้
1. เข้าไปที่ directory ที่เก็บไฟล์ CSV ตัวอย่างใน Video คือ C:\kicad\mylib
2. เปิด command shell แล้วใช้คำสั่งดังนี้ > kipart esp-12e.csv -s num -f -o esp8266-12e.lib -w
 |
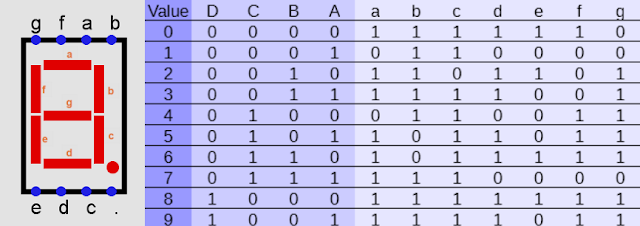
| รูปที่ 4 การเรียกใช้ Kipart |
Kipart esp-12e.csv = ให้ Kipart อ่านไฟล์ esp-12e.csv (ถ้าเป็น Zip file ใช้ esp-12e.zip)
-s num = sort by number
-f = ให้ใช้ fuzzy match มันจะถือว่า r ,rht, ri (กรณีพิพม์ไม่ถูกต้อง) เป็น right
-o esp8266-12e.lib = output file ให้ชื่อว่า esp8266-12e.lib
-w = เขียนทับไฟล์ที่มีอยู่แล้ว
ถ้าหากไม่คิดจะสร้างอะไรพิศดารหรือนอกเหนือไปจากนี้ การใช้คำสั่ง
“ Kipart ชื่อ CSV file.csv -s num -f -o ชื่อ lib file .lib -w “ ก็เพียงพอ
สามารถใส่ Path directory ได้ เช่น c:\kicad\share\kicad\library\ ชื่อ lib file .lib แต่ระวังพลาดไปเขียนทับ library ที่มีอยู่ (-w parameter จะทำให้มันเขียนทับไฟล์ โดยไม่มีการถาม)