การออกแบบ วงจรลบเลขฐานสอง

วงจรลบ (subtraction circuit)

ในการลบเลขฐานสอง แบบ 1 บิท เช่น A = 0  B = 1  ให้  X = A – B
 เราจะได้ว่า  X =  0 - 1   ไม่สามารถลบได้ ต้องยืมค่าจากบิทต่อไป ซึ่งมีค่า 1 0₂  จะแสดงการยืมค่าด้วย Bo  ที่บิทสูงสุด
ดังนั้น   X =  1 0₂ – 01₂ = 1  และ Bo = 1 ซึ่งแสดงว่าค่าที่ได้เป็นค่าลบ
ถ้าเราจะสร้างวงจรดิจิตอล เพื่อหาคำตอบ ของ A – B แบบ 1 บิทนี้ มันจะต้องสอดคล้องกับค่า A และ B ที่มีโอกาศจะเป็นไปได้ ทั้งหมด ตาม Truth table ในรูปที่ 4  ซึ่งเราจะได้วงจรดังนี้
X =  A XOR B  และ  Bo =  A' and B     ;    '  แสงการ NOT หรือ Invert ค่า
ลองทดสอบ กรณี  A = 0   และ B = 1 
X = 0 XOR 1  = 1     Bo = 1 and 1 =  1    ได้ค่าตรงตามตรารางค่าความจริง

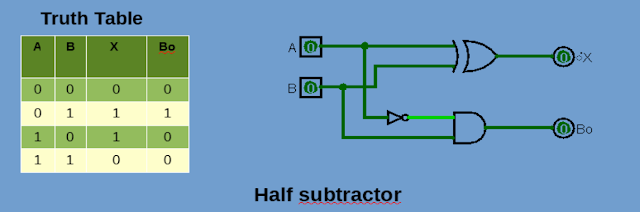รูปที่ 4 วงจรลบแบบไม่มีการยืม Half subtractor

ก่อนที่เราจะว่ากันด้วยหลักการทางคณิตศาสตร์ เรามาดูวิธีการสร้างจริงในทางปฎิบัติ ซึ่งเราใช้โปรแกรมในการช่วยออกแบบ Logisim  โดยเราจะให้ Logisim สร้างวงจรตาม Truth table ที่เรากำหนด

ถ้าเราจะแก้สมการนี้ X = 4,321 x 23 + 121/2 -7  ในปัจจุบันนี้เราคงไม่มาแก้ด้วยการคิดเอง หรือเขียนบนกระดาษ
เราคงจะเปิด App ในมือถือ หรือไม่ก็ใช้เครื่องคิดเลขในการหาคำตอบ  เราจะแก้คำตอบโดยการคิดเอง ก็ต่อเมื่อเป็น การเรียนการสอนเท่านั้น เช่น เดียวกัน ที่เราใช้ Logisim  เพราะในทางปฏิบัติ  ถ้าวงจรซับซ้อนมาก  เราคงไม่มานั่งทำ K-Map  หรือ  Karnaugh map ซึ่งแม้นเป็นวิธีการสร้างวงจรตรรกะ ที่รวดเร็วและง่ายต่อการเข้าใจ  ซึ่งมันอาจจำเป็นในการเรียน การสอน แต่ในทางปฏิบัติ  มี Tool หรือ เครื่องมืออยู่แล้ว  เราไม่ควรไปเสียเวลาทำเอง เพราะโอกาสพลาดมีเยอะ และยังไงเราก็ต้องต่อวงจรทดลองอยู่ ดี  ทางที่ดี ก็ให้ Tool มันสร้าง แล้วมาดัดแปลงแก้ไข ให้ดีขึ้น
หมายเหตุ
    • วงจรที่ Logisim สร้างขึ้น มันเป็นวงจรทางทฤษฎี ไม่ใช่ทางปฏิบัติ กล่าวคือ มันจะถือว่า เกจท์ (gate) หรืออุปกรณ์ ไม่มี Delay ภายในวงจรเลย ซึ่งจริงๆ แล้วไม่มี เกจท์ หรืออุปกรณ์อีเลคโทรนิคส์ตัวใด ไม่มีการ Delay ภายในวงจร ในสมัยก่อน เกจท์ (gate) แบบต่างๆ เช่น AND,OR, NOT เป็นต้น มี Delay ภายในค่อนข้างมาก เทียบกับปัจจุบัน ดังนั้น จึงอาจมี Rule of thump หรือกฏเกณท์ง่ายๆ ว่า ห้ามต่อเกจท์ใดๆ อนุกรมกันเกิน 4 ตัว เนื่องจาก  สมมุตว่าเกจท์แต่ละตัวมี Propagation delay  เท่ากันแล้ว  ถ้าต่ออนุกรมแบบ 4 ตัว Delay ที่เกิดขึ้นจะเป็น 4 เท่า  อาจจะทำให้ Output ของมันเปลี่ยนแปลงช้าเกินไป ไม่ทันการทำงานของวงจรอื่น หรือ Clock ของวงจร กรณีวงจรที่มีการใช้ Clock  เช่น CPU
    • Propagation delay คือ เวลาที่ใช้ในการเปลี่ยนแปลงค่า output จน stableของอุปกรณ์นับตั้งแต่เริ่มป้อน input
    • และในทางปฎิบัติอีกเช่นกัน เราก็สามารถ สร้างวงจร Delay ใส่ไว้ให้กับ Logisim เพื่อให้มัน Simulate ได้แม่นยำขึ้น

และเช่นเดียวกัน เราได้วงจรลบแบบมีการยืม หรือ Full subtractor ตามรูปที่  5

รูปที่ 5 วงจรลบแบบที่มีการยืม Full subtractor

หากเราจะลบเลขฐานสอง หลายๆ บิท เช่น 4  bit เราสามารถใช้วงจร Full subtractor  แบบ 1 บิทมาต่อกันดังรูปที่ 6

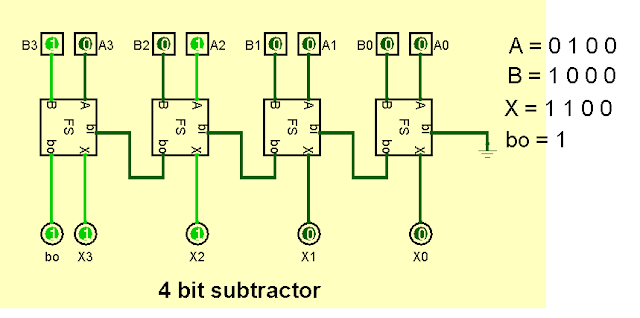รูปที่ 6 4 bit subtractor

จากรูปที่ 6: A = 0100₂ (4₁₀) - 1000₂ (8₁₀) ได้ X = 1100₂ (12₁₀ ) และ Bo = 1
ถ้าเอา Bo กับ X มาเรียงกันเป็น 1 1100₂ แล้วตีความตรงๆ เช่น  -12  หรือ16 + 12 = 28 ยิ่งไปกันใหญ่
Bo = 1 แสดงว่า มีการยืมค่ามาจากบิทถัดไป และค่าที่ได้เป็นค่าลบ  แต่จะมีค่าลบเท่าไรต้องเทียบว่าค่าที่ได้
อยู่ห่างจากบิทสูงสุดเท่าไร กรณีนี้ มีการยืมค่ามาจากบิทที่5 (บิท4) ซึ่งก็คือ   1 0000₂  = 16₁₀
มีอยู่แล้ว 4 ยืมมาอีก 16  A = 16 +4 ทำการลบแล้วเหลือเท่ากับ X = 12  แสดงว่ามันเกิดการติดลบหรือขาดอยู่เท่ากับ  1 0000₂   - 1100₂ = 0100₂  ได้คำตอบว่า A – B = - 0100₂
(วิธีที่ง่ายกว่า ก็คือ จับ X มาทำ 2’s complement แล้วใส่เครื่องหมายลบ ข้างหน้า)

ระบบ complement (complement system)  

แทนที่เราจะแสดงค่าลบ ด้วยเครื่องหมายลบ  เช่น - 0101₂   ในระบบนี้จะแสดงด้วย sign bit หรือ sign digit แทน  เช่น
- 0101₂     =  1011₂   ในระบบ 2’s complement system    1 เป็น sign bit บอกว่าเป็นลบ
       -5    =  95        ในระบบ 10’s complement system  9 เป็น sign bit บอกว่าเป็นลบ

เลขลบคือ อะไร ?  ในทางคณิตศาสตร์  เลขลบเกิดจากการคิดทิศทาง หรือบอกจำนวนที่ขาดอยู่  เช่น
-5  หมายถึง ขาดอยู่ 5 หรือ ในระบบแกน x,y มันหมายถึง ทิศทางที่ตรงกันข้ามกับค่าบวก ซึ่งจะอ้างอิงจากค่า 0
แต่ในระบบ  complement จะอ้างอิงจากจุด หรือหลักที่สูงกว่า เช่น

1011₂  ในระบบ 2’s complement system  จุดอ้างอิงมันอยู่ที่ 1000₂
  101₂  ในระบบ 2’s complement system  จุดอ้างอิงมันอยู่ที่ 100₂
    95   ในระบบ 10’s complement system  จุดอ้างอิงมันอยู่ที่ 10

ตัวอย่าง 10’s complement ของ 4,500  = 10,000-4,500 =5,500   (มันอยู่ห่างจาก 10,000 เท่ากับ -5,500)
ดังนั้น 1011₂  หมายความว่า มันอยู่ห่างจาก 1000₂  = 3 จะหาว่ามันห่างจาก 0 เท่าไร
ก็ต้องเอา   1000₂  มาลบด้วย 0011₂  อีกที จะได้ว่า = 5 (เมื่อคิดเครื่องหมาย = -5)

ในวงจรดิจิตอล จะนิยมใช้การลบด้วยการบวกเลขที่มีค่าเป็นลบ  เช่น A = 0100₂  B = 1000₂
A – B =   0100₂ + (-1000₂ )  ตัวเลขที่เป็นลบนี้ นิยมใช้  2’s complement ในการแสดงค่า
A – B =  A + 2’s complement  of B
2’s complement ของ 1000₂  = 1000₂ - 000 =  1000₂  (บังเอิญเท่ากันพอดี)
A – B =  0100₂ + 1000₂   = 1100₂   อยู่ในรูป 2’s complement  จะทำให้จุดอ้างอิงอยู่ที่ 0
A – B =  -(1000₂ – 100₂)  = -4

การหาค่า 2’s complement ในวงจรดิจิตอล จะทำโดยอาศัยหลักการที่ว่า
2’s complement  =   1’s complement  + 1
เมื่อ 1’s complement  คือการ invert ค่าจาก 0 เป็น 1 และ 1 เป็น 0 เช่น 1010₂   = 0101₂

ดังนั้นในวงจรดิจิตอล ถ้าเราจะหาคำตอบ ของ A-B ในรูป
A – B =  A + 1’s complement of B + 1 
เราสามารถใช้ วงจร Full adder ในการหาคำตอบ ด้วยการใส่ invertor หรือ not gate เข้าที่หน้า input ของ B  และให้  Carry in มีค่าเท่ากับ 1 หรือแรงดันระดับ High  ทำได้โดยต่อ Carry in ของ Full adder เข้ากับไฟเลี้ยงของวงจร  ส่วน Carry out จะต้องใส่ not gate เพิ่มเช่นกัน ตามรูปที่ 7 แต่จะได้วงจรลบแบบ Half  subtractor

รูปที่ 7 การลบแบบ 1 บิท โดยการใช้ Full adder

ดูจาก Truth table ในรูปที่ 7  แล้วมันมั่วหรือเปล่า  ไม่เห็นจะเหมือนกับในรูปที่ 2 หรือ รูปที่ 5 เลย  มันเหมือนรูปที่ 2 แน่นอน แต่ไม่เหมือนรูปที่ 5 เพราะมันเป็นแค่ Half subtractor   จะดูให้เหมือนเราต้องตัด กรณี Cin = 0 ออกให้หมด เพราะ Cin หรือ C จะถูกต่อเข้าที่ 1  หรือแรงดัน High ตลอดเวลา ไม่มีทางที่ Cin จะเท่ากับศูนย์  กรณีนี้ Co จะถือว่าเป็น  Bo  ถ้า Co = 1 แสดงว่าเกิดการยืม ค่าที่ได้เป็นค่าลบ (เลยต้องใส่ Not ให้เกิดทิศทางตรงกันข้าม)

รูปที่ 8 วงจรลบแบบ 4 บิท ที่สร้างมาจาก Full adder

อย่าไปสับสนกับวงจรในรูปที่ 6  อันนั้้นสร้างจาก Full subtractor รูปที่ 8 นี้สร้างจาก Full adder

008

Author & Editor

กรุณา อย่าเขียนความคิดเห็นที่ไม่เกี่ยวกับบทความ หรือข้อความที่พาดพิงผู้อื่นในลักษณะที่ทำให้เกิดความเสียหายต่อผู้อื่น