Karnoguh Map ( K-Map)

K-map เป็นวิธีการเขียน Truth table ที่ง่ายต่อการสังเกตุการเปลี่ยนแปลงของค่าในตาราง ทำให้สามารถแก้คำตอบของพีชคณิตบลูเลียน (ฺBoolean algebra) ได้อย่างรวดเร็ว เหมาะสมกับการแก้ปัญหาที่มีตัวแปรไม่เกิน 4 ตัว หรือมากที่สุดไม่เกิน 5 ตัว ถ้าจะใช้มากกว่านั้นจะนิยมใช้ Quine-Mccluskey method หรือ software ในการแก้ปัญหา เนื่องจาก จำนวนช่องในตารางมันมากเกินไปและยากต่อการสังเกตุ

รูปที่ 1 Truth table normal form (left)  K-Map form (middle) 

ในรูปที่ 1 ตารางด้านซ้าย เป็น Truth table ซึ่งเขียนในรูปปกติ  ตรงกลางเป็นการเขียนในรูป K-map  ส่วนขวาสุด เป็น บลูเลียน พีชคณิตในช่องต่างๆ  เมื่อสังเกตุดูตารางด้านซ้าย เราจะเห็นว่า เป็น OR Truth table เขียนเป็นสมการบลูเลียน ได้ดังนี้
F = A + B ; + แทนการ OR
ส่วนตาราง K-Map เรามีจุดสังเกตุดังนี้  ถ้ามองกรณีที่ F =1
ใน Row ที่ A = 1 นั้น ไม่ว่า B จะเท่ากับ 0 หรือ 1  F = 1 เสมอ  แสดงว่า F ไม่ขึ้นกับค่า B แต่ขึ้นกับ Aเท่านั้น F = A
ใน Col.ที่ B = 1 นั้น ไม่ว่า A จะเท่ากับ 0 หรือ 1  F = 1 เสมอ  แสดงว่า F  ไม่ขึ้นกับค่า A แต่ขึ้นกับ Bเท่านั้น F = B
เมื่อนำมารวมกัน ได้ F  = A + B

ข้อสังเกตุ
ในตาราง K-Map  ข้างบน ถ้าเรามองกรณีที่ F = 0 , A = 0 และ  B = 0    ถ้าจะใช้ K-Map จะตีความดังนี้
F´ = A´.B´   ;  F = (A´.B´)´  =  A + B   ( ´ แทนการ NOT   . แทนการ AND) 

กฏการเขียน K-Map
1. เขียน Input ที่เป็นไปได้ในแนว Rowกับ Column  และผลลัพท์หรือ Output คือค่าในตาราง
2. การเปลี่ยนสถานะของ Input จะต้องเปลี่ยนแปลงทีละตัว ไม่ว่าในแนว Row หรือ Col.   เช่น

รูปที่ 2 ตาราง K-map แบบ 2,3 และ 4 ตัวแปร

จากรูปที่ 2 ในตาราง K-map แบบ 3 และ 4 ตัวแปร เราจะเห็นว่า BC จะเขียนค่าเรียงตามลำดับได้ดังนี้
BC = 00 , 01, 11, 10  ในตาราง 3 ตัวแปรAB  และ CD = 00 , 01, 11, 10  ในตาราง 4 ตัวแปร
m0 ถึง m16 คือค่าของ F (A,B,C,D) ที่ตำแหน่งนั้น นิยมเรียก minterm  เช่น m5 = F (1,0,1) ในกรณี 3 ตัวแปร และ    m5 = F (0,1,0,1) ในกรณี 4 ตัวแปร
ทำไมไม่เรียงแบบเลขฐานสอง BC = 00 , 01 , 10, 11   จริงๆ ก็เรียงได้ไม่ได้ทำให้ F เปลี่ยนไป แต่จะสังเกตุความสัมพันธ์ยาก หรือจับกลุ่มยาก เมื่อตารางใหญ่ขึ้น แบบนี้ การเปลี่ยนสถานะจาก  BC =01 ไปเป็น BC = 10 มีการเปลี่ยนแปลงตัวแปรพร้อมกัน 2 ตัว คือ B จาก 0 ไป 1 และ C จาก 1 ไป 0

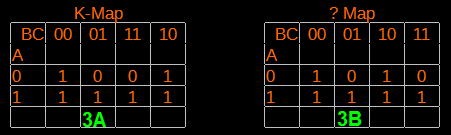รูปที่ 3 เปรียบเทียบ K-map กับ การ Map ที่เรียงค่าแบบเลขฐาน 2  

พิจารณา กรณีที่ F = 1
ใน Rowที่ A = 1 ใน รูป 3A และ 3B ได้ว่า การเปลี่ยนแปลงค่าของ B และ C ไม่มีผลต่อค่า F ดังนั้นได้ว่า F = A
ใน Rowที่ A = 0 ใน รูป 3A และ 3Bการเปลี่ยนค่าของ B จาก 0 ไป 1 ไม่มีผลต่อ F  แสดงว่า F ไม่ขึ้นกับ B  แต่จะให้ค่าตรงกันข้ามกับ input C ดังนั้น F = A´.C´ ( ´ แทนการ NOT   . แทนการ AND)
พิสูจน์โดยพีชคณิต บลูเลียน กรณี A = 0  และF = 1
F = A´.B´.C´ + A´.B.C´ =  A´.C´.(B´+B) =  A´.C´.1 = A´.C´
นำเอา F _A=0  + F _A=1  =  A´.C´+A
3. ให้จับกลุ่มตามค่าความจริงของ F  = 0 หรือ 1 อย่างใดอย่างหนึ่งเท่านั้น
4. การจับกลุ่มต้องจับในแนว ดิ่งหรือแนวนอน เท่านั้น ไม่สามารถจับกลุ่มตามแนวทแยงได้
5. ต้องจับกลุ่มให้อยู่ในรูป 2ⁿ  คือ 1 ,2,4,8.. ช่องเท่านั้น คือ จับกลุ่มทีละ 3,5,6,7... ไม่ได้
6. ต้องจับกลุ่มให้ใหญ่ที่สุด หรือครอบคุมตัวแปรให้มากที่สุด เพื่อให้จำนวนกลุ่มน้อยที่สุด
7.กลุ่มที่จับ สามารถทับซ้อนกัน
ตัวอย่างที่ 1 ให้ตาราง Truth table ของวงจรที่ต้องมีค่าตามรูปที่ 4

รูปที่ 4 Truth table ของวงจรที่ต้องการ  และ K-map

ทำตามกฏการเขียน K-Map
ข้อ 1 เขียน Input ในแนว Row กับ Col  ให้ผลลัพท์ที่ต้องการคือค่าในตาราง
ข้อ 2 การเปลี่ยนสถานะของ Input จะต้องเปลี่ยนแปลงทีละตัว ไม่ว่าในแนว Row หรือ Col.
จากข้อ 1 และ 2 เขียนตาราง K-Map ได้ตามรูปข้างบน
ข้อ 3-7 จับกลุ่มตามค่า F = 1  ในแนวนอน หรือแนวดิ่งให้มากที่สุด และสามารถทับซ้อนกันได้

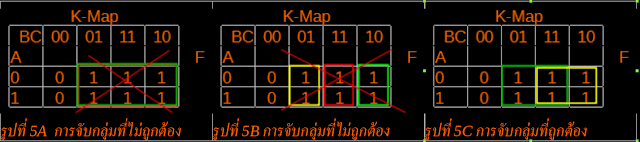รูปที่ 5 แสดงการจับกลุ่ม

รูป 5A จับไม่ถูกต้อง ตามกฏข้อ 5 คือ จับ ไม่อยู่ในรูป 2ⁿ  คือ 1 ,2,4,8  ช่อง
รูป 5Bจับไม่ถูกต้อง ตามกฏข้อ 6 คือ  ต้องจับกลุ่มให้ใหญ่ที่สุด แต่จำนวนช่องต้องอยู่ในรูป 1,2,4,8 เป็นต้น
ทั้ง 5A และ 5B เป็นการจับกลุ่มที่ไม่ดี แต่ก็ยังแก้ พีชคณิต บลูเลียนได้แต่ช้า
รูป 5C จับได้ถูกต้อง คือเป็นกลุ่มละ 4 ช่อง และมีพื้นที่ทับซ้อนกัน แต่ยอมได้ตามกฏข้อ 7

จากรูปที่ 5C  พิจารณาที่พื้นที่สีเขียว  A และ  B มีการเปลี่ยนแปลงค่า คือ 0 และ 1 แต่ไม่มีผลต่อการเปลี่ยนแปลงของค่า F หรือค่าความจริง ดังนั้นค่า F ไม่ขึ้นกับค่า A และ B แต่ขึ้นกับ C เท่านั้น คือ Cมีค่าเป็น 1 จะทำให้  F = 1
ดังนั้นบริเวณนี้ ได้ว่า  F  =  C

เพื่อความรวดเร็ว เราจะใช้วิธีดูว่า ค่าตัวแปรใด ในพื้นที่ที่เราจับกลุ่มไม่มีการเปลี่ยนแปลงค่า  แสดงว่า F ขึ้นกับตัวแปรนั้น  กรณีพื้นที่สีเขียว C ไม่มีการเปลี่ยนแปลงค่า F = C

จากรูปที่ 5C  พิจารณาที่พื้นที่สีเหลือง A และ  C  มีการเปลี่ยนแปลงค่า คือ 0 และ 1 ขณะที่ B ไม่เปลี่ยนแปลง และมีค่าเป็น 1 ดังนั้นบริเวณนี้ ได้ว่า  F  =  B
ดังนั้น F = B + C
ลองตรวจสอบคำตอบ กับ ตาราง K-map
ถ้า  B = 0 , C= 0  F = B+ C = 0  นั่นคือ ช่องที่ BC = 00 จะได้ F =0
ถ้า  B  และ  C ไม่เป็น 0 พร้อมกัน เช่น  ช่องที่ BC = 01,11 หรือ 10  จะได้ F =1

ตัวอย่างที่ 2 ให้ F( m5,m7,m13,m16) = 0 จงหาฟังก์ชั่น F
อย่างนี้บอกในรูป minterm  ตัวสูงสุด m16 แสดงว่า เป็นตาราง K-map แบบ 16 ช่อง ตามรูปที่ 2 ข้างบน  เขียนเป็นตาราง K-map ได้ดังนี้

รูปที่ 6 K-map F(m5,m7,m13,m16) = 0

ตามกฏข้อ 3- 7 จับกลุ่มตาม F = 1  และจับกลุ่มให้ใหญ่ที่สุดในรูป  1,2,4 ,8 หรือ 16

ตามกฏข้อ 6 จับกลุ่มให้ใหญ่ที่สุด และจำนวนกลุ่มน้อยที่สุด ทำได้ตามรูปคือ จับกลุ่มละ8  2กลุ่มตามรูป คือ กลุ่มสีเขียวและ กลุ่มสีแดง
ที่กลุ่มสีเขียว จะเห็นว่า A, C, D มีการเปลี่ยนค่า จาก 0 และ 1 แต่ B ไม่เปลี่ยนแปลงค่า  และมีค่าเป็น 0 ดังนั้นที่กลุ่มนี้ ได้ F = B´
ที่กลุ่มสีแดง จะเห็นว่า A, B, C มีการเปลี่ยนค่า จาก 0 และ 1 แต่ Dไม่เปลี่ยนแปลงค่า และมีค่าเป็น 0 ดังนั้นที่กลุ่มนี้ ได้ F = D´
ได้ว่า  F = B´ +  D´

ตัวอย่างการจับกลุ่มในรูปแบบต่างๆ

รูปที่ 7 แสดงตัวอย่างการจับกลุ่ม

รูปที่ 8 จับกลุ่มมากเกินไป

เปรียบเทียบ รูปที่ 7B กับ รูปที่ 8  ซึ่งกลุ่มสีเหลืองทับซ้อนกับ กลุ่มสีแดงและสีเขียวทั้งหมด  อย่างงี้ไม่จำเป็นต้องจับกลุ่มสีเหลือง เพราะ 1 ทุกตัวมีกลุ่มอยู่แล้ว และตาม กฏข้อที่ 6 ให้จับกลุ่มให้ได้น้อยที่สุด

พิสูจน์    รูป ที่ 7 B  F 1 = B´.D´ + A.B   เท่ากับ รูปที่ 8  F2  = B´.D´ + A.B +A.D´ 
  ถ้า  A = 0  F1 =   B´.D´    F2  = B´.D´
  ถ้า  A = 1  F 1 = B´.D´ + B    F2  = B´.D´ +D´ + B   =   D´.(B´+1) + B  =  B´.D´ + B

ตัวอย่างที่ 3 ให้ออกแบบวงจร  BCD to 7 Segment  Display decoder

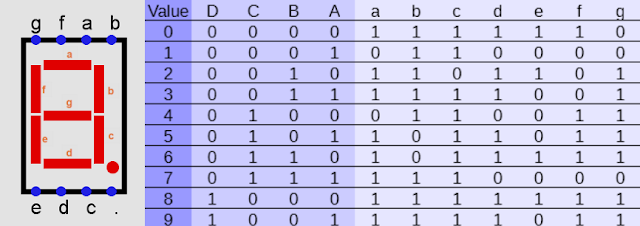รูปที่ 9  BCD to 7 Segment display decoder truth table

จากรูปที่ 9 เป็นตัวแสดงผลด้วย LED แบบ 7 segments 
ถ้าเราจะแสดงเลข 0 จะต้องให้ segment a,b,c,d,e, และ f ติด หรือมีแรงดันเป็น High
ถ้าเราจะแสดงเลข 1 จะต้องให้ segment b และ c ติด หรือมีแรงดันเป็น High

กรณีใช้  K-map แก้ปัญหา  จากตารางค่าความจริงรูปที่ 9 ค่า BCD ที่เป็นไปได้มีค่า 0- 9 ดังนั้นถ้าใช้ K-map แบบ 4 ตัวแปร เทอมที่ 10-15 จะไม่มีโอกาศเกิดขั้น จะใช้ don’t care condition (x)

ที่ segment a (a Column) มันจะไม่ติดเมื่อ ค่า BCD เป็น 1 หรือ4  หรือค่า DCBA = 0001 หรือ 0100

กรณีคิดจาก a = 1 หรือมันจะติด กลุ่มสีเขียว a = B กลุ่มสีแดง a = D กลุ่มสีเหลือง a = C´.A´ กลุ่มสีส้ม a = C.A เพราะฉะนั้น a = B + D + C´.A´ + C.A ( C´.A´ + C.A สามารถแทนได้ด้วย C XOR A)

ที่ segment b (b column) มันจะไม่ติดเมื่อ ค่า BCD เป็น 5 หรือ 6

กลุ่มสีเขียว a = C กลุ่มสีแดง a = D กลุ่มสีเหลือง a = B´.A´ กลุ่มสีส้ม a = B.A เพราะฉะนั้น b = C+ D + B´.A´ + B.A

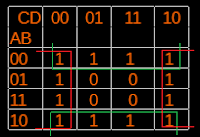
ที่ segment c (c column) ที่ segment d (d column) ที่ segment e(e column)

c = D+C+A+B´ d = D+B.A´+C´.A´+ C´.B+C.B´.A e = B.A´+C´.A´ หมายเหตุ ที่ Segment e ไม่ต้องจับกลุ่ม x ที่ไม่มี 1 อยู่เนื่องจากมันไม่มีโอกาศเกิดขึ้น (เช่น แถวDC = 11) ที่ segment f (f column) ที่ segment g (g column)

f = D+C.B´+B´A´+C.A´ g = D+C.B´+B.A´+C´B

008

Author & Editor

กรุณา อย่าเขียนความคิดเห็นที่ไม่เกี่ยวกับบทความ หรือข้อความที่พาดพิงผู้อื่นในลักษณะที่ทำให้เกิดความเสียหายต่อผู้อื่น